![[Hướng Dẫn] Cách Nén File & Cách Giải Nén File [RAR, ZIP, PDF] 2024](https://camnangquanly.edu.vn/wp-content/uploads/2024/05/cach-giai-nen-file-tren-may-tinh-1-150x150.jpg "[Hướng Dẫn] Cách Nén File & Cách Giải Nén File [RAR, ZIP, PDF] 2024")
Bài viết này Vted trình bày và giới thiệu đến bạn đọc Công thức tính thể tích của một khối chóp cụt và một số ví dụ minh hoạ. Công thức này cho phép tính thể tích một số khối đa diện mức độ vận dụng, vận dụng cao.
Hình chóp cụt
Cho hình chóp $S.{{A}_{1}}{{A}_{2}}…{{A}_{n}}.$ Một mặt phẳng không đi qua $S$ và song song với mặt phẳng đáy, cắt các cạnh $S{{A}_{1}},S{{A}_{2}},…,S{{A}_{n}}$ tương ứng tại ${{B}_{1}},{{B}_{2}},…,{{B}_{n}}.$
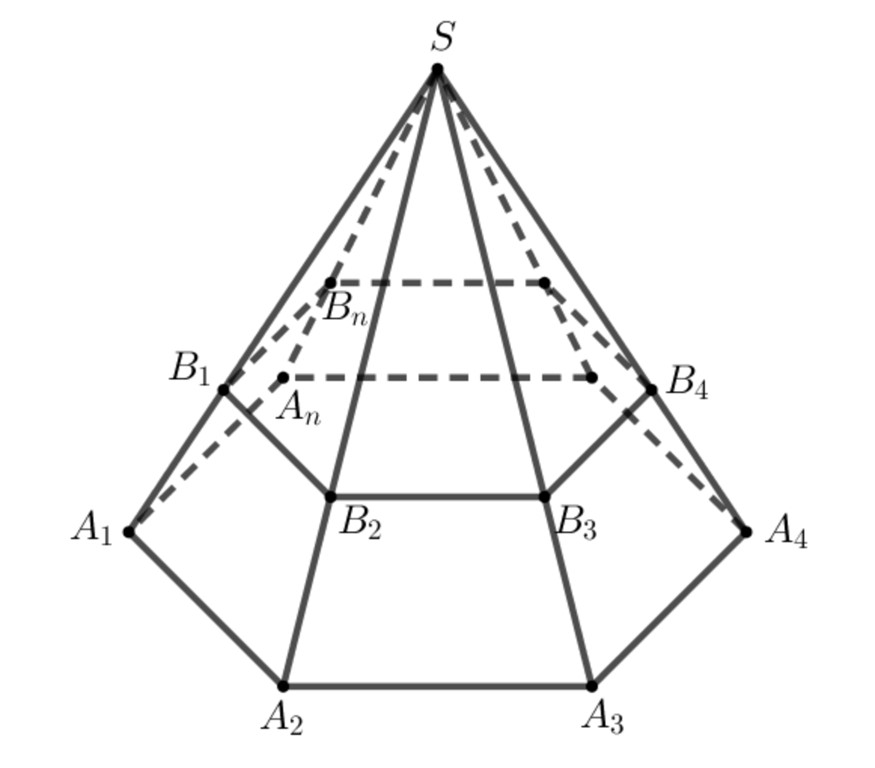
+ Hình gồm các đa giác ${{A}_{1}}{{A}_{2}}…{{A}_{n}},{{B}_{1}}{{B}_{2}}…{{B}_{n}}$ và các hình thang ${{A}_{1}}{{A}_{2}}{{B}_{2}}{{B}_{1}},{{A}_{2}}{{A}_{3}}{{B}_{3}}{{B}_{2}},…,{{A}_{n}}{{A}_{1}}{{B}_{1}}{{B}_{n}}$ được gọi là một hình chóp cụt, kí hiệu là ${{A}_{1}}{{A}_{2}}…{{A}_{n}}.{{B}_{1}}{{B}_{2}}…{{B}_{n}}.$
Một cách đơn giản, hình chóp cụt được tạo thành từ hình chóp $S.{{A}_{1}}{{A}_{2}}…{{A}_{n}}$ sau khi cắt đi hình chóp $S.{{B}_{1}}{{B}_{2}}…{{B}_{n}}.$
+ Các đa giác ${{A}_{1}}{{A}_{2}}…{{A}_{n}},{{B}_{1}}{{B}_{2}}…{{B}_{n}}$ được gọi là hai mặt đáy, các hình thang ${{A}_{1}}{{A}_{2}}{{B}_{2}}{{B}_{1}},{{A}_{2}}{{A}_{3}}{{B}_{3}}{{B}_{2}},…,{{A}_{n}}{{A}_{1}}{{B}_{1}}{{B}_{n}}$ được gọi là các mặt bên. Các đoạn thẳng ${{A}_{1}}{{B}_{1}},{{A}_{2}}{{B}_{2}},…,{{A}_{n}}{{B}_{n}}$ được gọi là các cạnh bên, các cạnh của mặt đáy được gọi là các cạnh đáy.
+ Khoảng cách giữa hai mặt đáy được gọi là chiều cao của hình chóp cụt.
Hình chóp cụt đều
Hình chóp cụt đều là hình chóp cụt có hai đáy là các đa giác đều và độ dài các cạnh bên bằng nhau.
Thể tích của khối chóp cụt
Khi cắt khối chóp bởi một mặt phẳng song song với đáy thì mặt phẳng đó chia khối chóp đã cho thành hai khối đa diện, khối bên trên là khối chóp và khối bên dưới được gọi là khối chóp cụt.
Thể tích của khối chóp cụt có diện tích hai đáy lần lượt là ${{S}_{1}},{{S}_{2}}$ và chiều cao bằng $h$ (khoảng cách giữa hai đáy) là [V=dfrac{h({{S}_{1}}+{{S}_{2}}+sqrt{{{S}_{1}}{{S}_{2}}})}{3}.]
Xem thêm Công thức tính thể tích, diện tích xung quanh, diện tích toàn phần của khối nón cụt
Video bài giảng: Thể tích khối chóp cụt và ứng dụng
>>Xem thêm Công thức tổng quát tính thể tích của một khối tứ diện bất kì và các trường hợp đặc biệt
Link đăng ký: https://bit.ly/3Xd5EA5
PRO X: Luyện thi THPT 2024 Môn Toán (Luyện mọi dạng bài từ cơ bản đến 9 điểm)
XMAX: Luyện mọi dạng bài vận dụng cao Môn Toán 2024 (Mức 9+)
LIVE X: Tổng ôn kiến thức và chữa đề dự đoán 2024 Môn Toán (100 ngày)
XPLUS: Luyện giải đề thi THPT 2024 Môn Toán
Các khoá học được sử dụng kể từ ngày đăng kí đến khi kì thi THPT 2024 kết thúc.
Ví dụ 1: Cho hình lăng trụ tam giác đều $ABC.{A}'{B}'{C}’$ có tất cả các cạnh bằng $a.$ Gọi $M,text{ }N$ lần lượt là trung điểm của cạnh $AB$ và ${B}'{C}’.$ Mặt phẳng $left( {A}’MN right)$ cắt cạnh $BC$ tại $P.$ Tính thể tích $V$ của khối đa diện $MBP.{A}'{B}’N.$
Giải. Gọi $S$ là giao điểm của ${A}’M$ và $B{B}’$, khi đó $P$ là giao điểm $SN$ và $BC.$
Ta có $dfrac{MP}{{A}’N}=dfrac{BP}{{B}’N}=dfrac{BM}{{A}'{B}’}=dfrac{1}{2}Rightarrow Delta MBP$ đồng dạng với $Delta {A}'{B}’N$ theo tỷ số bằng $dfrac{1}{2}.$
Khối đa diện $MBP.{A}'{B}’N$ là khối chóp cụt có chiều cao $h=B{B}’=a$ và diện tích hay đáy là ${{S}_{1}}={{S}_{{A}'{B}’N}}=dfrac{1}{2}{{S}_{{A}'{B}'{C}’}}=dfrac{{{a}^{2}}sqrt{3}}{8},{{S}_{2}}={{S}_{MBP}}=dfrac{1}{4}{{S}_{{A}'{B}’N}}=dfrac{{{a}^{2}}sqrt{3}}{32}.$
Vậy ${{V}_{MBP.{A}'{B}’N}}=dfrac{h}{3}left( {{S}_{1}}+{{S}_{2}}+sqrt{{{S}_{1}}{{S}_{2}}} right)=dfrac{a}{3}left( dfrac{{{a}^{2}}sqrt{3}}{8}+dfrac{{{a}^{2}}sqrt{3}}{32}+sqrt{dfrac{{{a}^{2}}sqrt{3}}{8}dfrac{{{a}^{2}}sqrt{3}}{32}} right)=dfrac{7sqrt{3}{{a}^{3}}}{96}.$
Chọn đáp án B.
Các em xem lại Bài giảng Thể tích khối chóp cụt và ứng dụng khoá PRO X.
Cách 2: Ta có $dfrac{{{V}_{SMBP}}}{{{V}_{S{A}'{B}’N}}}=dfrac{SM}{S{A}’}.dfrac{SB}{S{B}’}.dfrac{SP}{SN}={{left( dfrac{SB}{S{B}’} right)}^{3}}=dfrac{1}{8}$$Rightarrow {{V}_{MBP.{A}'{B}’N}}=dfrac{7}{8}{{V}_{S{A}'{B}’N}}.$
Ta có ${{V}_{S{A}'{B}’N}}=dfrac{1}{3}S{B}’.{{S}_{Delta {A}'{B}’N}}$$=dfrac{1}{3}S{B}’.dfrac{1}{2}{A}'{B}’.{B}’Nsin 60{}^circ $$=dfrac{1}{6}2a.a.dfrac{a}{2}sin 60{}^circ $$=dfrac{{{a}^{3}}sqrt{3}}{12}$.
$Rightarrow {{V}_{MBP.{A}'{B}’N}}=dfrac{7}{8}{{V}_{S{A}'{B}’N}}=dfrac{7{{a}^{3}}sqrt{3}}{96}$.
Chọn đáp án B.
Các em xem lại Bài giảng Tỷ số Thể tích khoá PRO X.
Ví dụ 2: Cho một chậu nước hình chóp cụt đều (hình vẽ) có chiều cao bằng $3dm,$ đáy là lục giác đều, độ dài cạnh đáy lớn bằng $2dm$ và độ dài cạnh đáy nhỏ bằng $1dm.$ Tính thể tích của chậu nước
A. $dfrac{21sqrt{3}}{2}d{{m}^{3}}.$
B. $dfrac{21sqrt{2}}{4}d{{m}^{3}}.$
C. $dfrac{21}{2}d{{m}^{3}}.$
D. $dfrac{21sqrt{6}}{4}d{{m}^{3}}.$
Giải. Diện tích đáy của chậu bằng ${{S}_{1}}=6left( dfrac{{{2}^{2}}sqrt{3}}{4} right)=6sqrt{3},{{S}_{2}}=6left( dfrac{{{1}^{2}}sqrt{3}}{4} right)=dfrac{3sqrt{3}}{2}.$
Chiều cao của chậu bằng $h=3.$
Thể tích của chậu bằng ${{V}_{0}}=dfrac{h}{3}left( {{S}_{1}}+{{S}_{2}}+sqrt{{{S}_{1}}{{S}_{2}}} right)=dfrac{3}{3}left( 6sqrt{3}+dfrac{3sqrt{3}}{2}+sqrt{6sqrt{3}dfrac{3sqrt{3}}{2}} right)=dfrac{21sqrt{3}}{2}d{{m}^{3}}.$ Chọn đáp án A.
Note: Diện tích lục giác đều gấp 6 lần diện tích tam giác đều có cùng độ dài cạnh.
Ví dụ 3: Cho lăng trụ đứng $ABC.{A}'{B}'{C}’$ có đáy là tam giác đều cạnh $a,A{A}’=2a.$ Gọi $M,N$ lần lượt là trung điểm các cạnh $A{A}’,B{B}’$ và $G$ là trọng tâm tam giác $ABC.$ Mặt phẳng $(MNG)$ cắt $CA,CB$ lần lượt tại $E,F.$ Thể tích của khối đa diện có sáu đỉnh $A,B,M,N,E,F$ bằng
Giải. Do $MN//(ABC)Rightarrow (MNG)cap (ABC)=EF//AB.$ Gọi $P$ là trung điểm $C{C}’.$ Ta có $MNP.EFC$ là một chóp cụt.
$begin{gathered} {V_{ABNMEF}} = {V_{ABC.MNP}} – {V_{MNP.EFC}} = dfrac{1}{2}{V_{ABC.A’B’C’}} – dfrac{{CP}}{3}left( {{S_{MNP}} + {S_{EFC}} + sqrt {{S_{MNP}}{S_{EFC}}} } right) = dfrac{1}{2}left( {dfrac{{sqrt 3 {a^2}}}{4}} right)left( {2a} right) – dfrac{a}{3}left( {dfrac{{sqrt 3 {a^2}}}{4} + {{left( {dfrac{2}{3}} right)}^2}dfrac{{sqrt 3 {a^2}}}{4} + sqrt {dfrac{{sqrt 3 {a^2}}}{4}{{left( {dfrac{2}{3}} right)}^2}dfrac{{sqrt 3 {a^2}}}{4}} } right) = dfrac{{2sqrt 3 {a^3}}}{{27}}. end{gathered} $
Trong đó ${{S}_{MNP}}={{S}_{ABC}}=dfrac{sqrt{3}}{4}{{a}^{2}};dfrac{CE}{CA}=dfrac{CF}{CB}=dfrac{CG}{CI}=dfrac{2}{3}Rightarrow Delta CEFbacksim Delta CAB$ tỉ số $dfrac{2}{3}Rightarrow {{S}_{CEF}}={{left( dfrac{2}{3} right)}^{2}}{{S}_{CAB}}={{left( dfrac{2}{3} right)}^{2}}dfrac{sqrt{3}}{4}{{a}^{2}}.$
Hoặc [{{S}_{CEF}}=dfrac{1}{2}CE.CF.sin widehat{ECF}=dfrac{1}{2}.dfrac{2a}{3}.dfrac{2a}{3}.dfrac{sqrt{3}}{2}=dfrac{sqrt{3}{{a}^{2}}}{9}.] Chọn đáp án D.
Ví dụ 4: Cho lăng trụ $ABC.{A}'{B}'{C}’$ có thể tích bằng $24$. Gọi $M,, N$ và $P$ lần lượt là các điểm nằm trên các cạnh ${A}'{B}’,,, {B}'{C}’$ và $BC$ sao cho $M$ là trung điểm của ${A}'{B}’$, ${B}’N=dfrac{3}{4}{B}'{C}’$ và $BP=dfrac{1}{4}BC.$ Đường thẳng $NP$ cắt đường thẳng $B{B}’$ tại $E$ và đường thẳng $EM$ cắt đường thẳng $AB$ tại $Q.$ Thể tích của khối đa diện lồi $AQPC{A}’MN{C}’$ bằng
Giải. Đặt $S,h$ lần lượt là diện tích đáy và chiều cao của lăng trụ đã cho ta có $S.h=24$ và
${{V}_{AQPC{A}’MN{C}’}}={{V}_{ABC.{A}'{B}'{C}’}}-{{V}_{BPQ.{B}’NM}}.$ Trong đó $BPQ.{B}’NM$ là chóp cụt có chiều cao $h.$
Ta có $dfrac{EB}{E{B}’}=dfrac{EP}{EN}=dfrac{EQ}{EM}=dfrac{BP}{{B}’N}=dfrac{BQ}{{B}’M}=dfrac{PQ}{NM}=dfrac{1}{3}.$ Do đó hai tam giác $Delta BPQbacksim Delta {B}’NM$ theo tỷ số $k=dfrac{1}{3}.$
Suy ra ${{S}_{{B}’NM}}=dfrac{{B}’N}{{B}'{C}’}times dfrac{{B}’M}{{B}'{A}’}S=dfrac{3}{4}.dfrac{1}{2}S=dfrac{3}{8}S;{{S}_{BPQ}}={{left( dfrac{1}{3} right)}^{2}}{{S}_{{B}’NM}}=dfrac{1}{24}S.$
Vì vậy ${{V}_{BPQ.{B}’NM}}=dfrac{h}{3}left( dfrac{3}{8}S+dfrac{1}{24}S+sqrt{dfrac{3}{8}Stimes dfrac{1}{24}S} right)=dfrac{13}{72}S.h=dfrac{13}{72}times 24=dfrac{13}{3}Rightarrow {{V}_{AQPC{A}’MN{C}’}}=24-dfrac{13}{3}=dfrac{59}{3}.$ Chọn đáp án C.
Ví dụ 5: Cho khối lăng trụ đứng $ABC.{A}'{B}'{C}’$ có đáy $ABC$ là tam giác vuông cân tại $C,AB=2a$ và góc tạo bởi hai mặt phẳng $(AB{C}’)$ và $(ABC)$ bằng $60{}^circ .$ Gọi $M,N$ lần lượt là trung điểm của ${A}'{C}’$ và $BC.$ Mặt phẳng $(AMN)$ chia khối lăng trụ đã cho thành hai khối đa diện. Khối đa diện có thể tích nhỏ hơn bằng
Giải. Gọi $E$ là trung điểm $AB Rightarrow left{ begin{array}{l} AB bot CC’ AB bot CE end{array} right. Rightarrow AB bot (CEC’) Rightarrow widehat {C’EC} = left( {(ABC’),(ABC)} right) = {60^0} Rightarrow CC’ = CEsqrt 3 = asqrt 3 .$
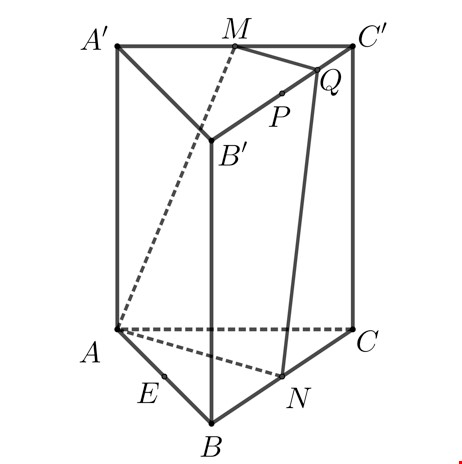
Vì $(ABC)//({A}'{B}'{C}’)Rightarrow (AMN)cap ({A}'{B}'{C}’)=MQ//AN.$
Khối đa diện $ANC.MQ{C}’$ có thể tích nhỏ hơn và là là khối chóp cụt có ${{S}_{1}}={{S}_{ANC}}=dfrac{1}{2}{{S}_{ABC}}=dfrac{1}{2}{{a}^{2}},{{S}_{2}}={{S}_{MQ{C}’}}=dfrac{1}{4}{{S}_{ANC}}=dfrac{1}{8}{{a}^{2}};h=C{C}’=sqrt{3}a.$
Vì vậy ${{V}_{ANC.MQ{C}’}}=dfrac{h}{3}left( {{S}_{1}}+{{S}_{2}}+sqrt{{{S}_{1}}{{S}_{2}}} right)=dfrac{sqrt{3}a}{3}left( dfrac{1}{2}{{a}^{2}}+dfrac{1}{8}{{a}^{2}}+sqrt{dfrac{1}{2}{{a}^{2}}dfrac{1}{8}{{a}^{2}}} right)=dfrac{7sqrt{3}{{a}^{3}}}{24}.$ Chọn đáp án A.Xem thêm Công thức tổng quát tính bán kính mặt cầu ngoại tiếp khối tứ diện và các trường hợp đặc biệt
Câu hỏi tự luyện: Cho khối lập phương $ABCD.{A}'{B}'{C}'{D}’$ có độ dài cạnh bằng $a.$ Mặt phẳng chứa đường thẳng $C{D}’$ tạo với mặt phẳng $left( {A}'{B}'{C}'{D}’ right)$ góc $alpha $ với $tan alpha =dfrac{sqrt{5}}{2}$ chia khối lập phương thành hai khối đa diện có thể tích ${{V}_{1}},{{V}_{2}}text{ }left( {{V}_{1}}>{{V}_{2}} right).$ Khi đó ${{V}_{1}}$ bằng
A. $dfrac{7}{24}{{a}^{3}}.$
B. $dfrac{7}{12}{{a}^{3}}.$
C. $dfrac{17}{24}{{a}^{3}}.$
D. $dfrac{10}{17}{{a}^{3}}.$
